The most copied StackOverflow snippet of all time is flawed!

by Andreas Lundblad, 2019-12-02

In a recent study titled Usage and Attribution of Stack Overflow Code Snippets in GitHub Projects, an answer I wrote almost a decade ago was found to be the most copied snippet on Stack Overflow. Ironically it happens to be buggy.

A Long Long Time Ago…

Back in 2010 I was sitting in my office and doing what I wasn’t supposed to be doing: code golfing and chasing reputation on Stack Overflow.

The following question got my attention: How do you print a byte count in a human readable format? That is, how do you format something like 123,456,789 bytes as “123.5 MB”.

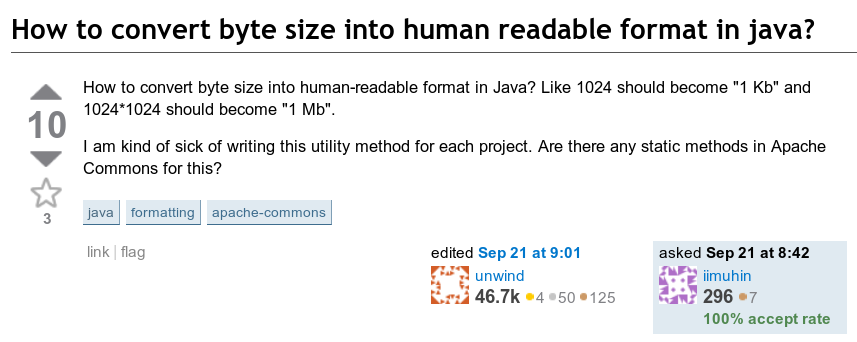
The good ol’ 2010 look, courtesy the Wayback Machine.

The implicit spec here is that the resulting string should have a value between 1 and 999.9 followed by a suffix with an appropriate magnitude.

One answer had already been posted. The code in that answer was based on a loop. The idea was simple: Try all magnitudes, going from the largest (EB = 10¹⁸ bytes) down to the smallest (B = 1 byte) and use the first one that is smaller than the number of bytes. In pseudo code it looks something like this:

suffixes   = [ "EB", "PB", "TB", "GB", "MB", "kB", "B" ]
magnitudes = [ 1018, 1015, 1012, 109, 106, 103, 100 ]
i = 0
while (i < magnitudes.length && magnitudes[i] > byteCount)
    i++
printf("%.1f %s", byteCount / magnitudes[i], suffixes[i])

Usually when there’s a correct answer posted that already has a positive score, it’s hard to catch up with it. In Stack Overflow lingo it’s referred to as the Fastest Gun in the West Problem. In this case the existing answer had a few flaws, so I still saw an opportunity to top it. At the very least, the loop based code could be cleaned up significantly.

This is Algebra, I know this!

Then it hit me. The kB, MB, GB, … suffixes are nothing but powers of 1000 (or 1024 in IEC standard) which means it should be possible to compute the right suffix using logarithms instead of a loop.

Based on this idea, I posted the following:

public static String humanReadableByteCount(long bytes, boolean si) {
    int unit = si ? 1000 : 1024;
    if (bytes < unit) return bytes + " B";
    int exp = (int) (Math.log(bytes) / Math.log(unit));
    String pre = (si ? "kMGTPE" : "KMGTPE").charAt(exp-1) + (si ? "" : "i");
    return String.format("%.1f %sB", bytes / Math.pow(unit, exp), pre);
}

Granted it’s not very readable and log / pow probably makes it less efficient than other solutions. But there were no loops and almost no branching which I thought was pretty neat.

All I could do now was to wait and see if the community would appreciate the answer. Little did I know that this would become the most copied snippet on Stack Overflow.

A Study on Attribution

Fast forward to 2018. A PhD student by the name Sebastian Baltes publishes a paper in the journal of Empirical Software Engineering. The title is Usage and Attribution of Stack Overflow Code Snippets in GitHub Projects and it basically tries to answer one question: Is Stack Overflow’s CC BY-SA 3.0 license respected? I.e. to what extent is proper attribution given, when copying code from Stack Overflow.

As part of their analysis they extracted code snippets from the Stack Overflow data dump and matched them against code from public GitHub repos. Quoting the abstract:

We present results of a large-scale empiricalstudy analyzing the usage and attribution of non-trivial Java code snippetsfrom SO answers in public GitHub (GH) projects.

(Spoiler alert: No, most people do not include proper attribution.)

In the paper, they include the following table:

That answer at the top with id 3758880 happens to be the answer I had posted eight years earlier. At this point the answer had over a hundreds of thousands of views and over a thousand upvotes.

A quick search on GitHub indeed shows thousands of occurrences of humanReadableByteCount.

To check if you happen to have the code in a locally checked out repo:

$ git grep humanReadableByteCount

The Bug

I bet you’ve already given it some thought. What is that bug in the code snippet?

Here it is again:

public static String humanReadableByteCount(long bytes, boolean si) {
    int unit = si ? 1000 : 1024;
    if (bytes < unit) return bytes + " B";
    int exp = (int) (Math.log(bytes) / Math.log(unit));
    String pre = (si ? "kMGTPE" : "KMGTPE").charAt(exp-1) + (si ? "" : "i");
    return String.format("%.1f %sB", bytes / Math.pow(unit, exp), pre);
}

After exabytes, 10¹⁸, comes zettabytes, 10²¹. Could it be that a really large input causes an index out of bounds on the "kMGTPE" string? Nope. The maximum long value is 2⁶³ - 1 ≈ 9.2 × 10¹⁸, so no long value will ever go beyond EB.

Could it be a mix-up between SI and binary? Nope. There was a mix-up in an early version of the answer, but that was fixed rather quickly.

Can exp end up being 0 causing charAt(exp-1) to fail? Nope. The first if-statement covers that case. The exp value will always be at least 1.

Could there be some weird rounding error in the output? Now we’re getting there…

Lots of 9’s

The solution works all the way up until it approaches 1 MB. When given 999,999 bytes as input, the result (in SI mode) is "1000.0 kB". While it is true that 999,999 is closer to 1,000 × 1000¹ than it is to 999.9 × 1000¹, the 1,000 “significand” is out of range according to spec. The correct result is "1.0 MB".

FWIW, all 22 answers posted, including the ones using Apache Commons and Android libraries, had this bug (or a variation of it) at the time of writing this article.

So how do we fix this? First of all, we note that the exponent (exp) should change from ‘k’ to ‘M’ as soon as the number of bytes is closer to 1 × 1,000² (1 MB) than it is to 999.9 × 1000¹ (999.9 k). This happens at 999,950. Similarly, we should switch from ‘M’ to ‘G’ when we pass 999,950,000 and so on.

To achieve this we calculate this threshold and bump exp if bytes is larger. (For the binary case, this threshold is not an integer, se we need to ceil the result.)

if (bytes >= Math.ceil(Math.pow(unit, exp) * (unit - 0.05)))
    exp++;

With this change the code works well all the way up until the byte count approaches 1 EB.

Even More 9’s

Given the input 999,949,999,999,999,999 the result is now 1000.0 PB while correct result is 999.9 PB. Mathematically the code is accurate, so what’s going on here?

At this point we’re running into the precision limitations of a double.

double a = Double.MAX_VALUE;
double b = a - Long.MAX_VALUE;
System.err.println(a == b);  // prints true

There are two problematic computations:

• The division in the String.format argument, and
• The threshold for bumping exp.

We could switch to BigDecimal, but where’s the fun in that?! Besides, it gets messy anyway because there’s no BigDecimal log function in the standard API.

Scaling down intermediate values

For the first issue we can scale down the bytes value to a range where the the precision is better, and adjust exp accordingly. The end result is rounded anyway, so it doesn’t matter that we’re throwing out the least significant digits.

if (exp > 4) {
    bytes /= unit;
    exp--;
}

Adjusting the least significant bits

For the second issue, we do care about the least significant bits (999,949,99…9 and 999,950,00…0 should end up with different exponents) so this issue calls for a different solution.

First we note that there are 12 different possible values for the threshold (6 for each mode), and only one of them ends up faulty. The faulty result can be uniquely identified by the fact that it ends with D00₁₆. If this is the case we simply adjust it to the correct value.

long th = (long) Math.ceil(Math.pow(unit, exp) * (unit - 0.05));
if (exp < 6 && bytes >= th - ((th & 0xFFF) == 0xD00 ? 51 : 0))
    exp++;

Since we rely on specific bit patterns in floating-point results, we slap on strictfp to ensure it works regardless of the hardware running the code.

Negative input

It’s unclear under what circumstances a negative byte count could be relevant, but since Java doesn’t have unsigned long, we better deal with it. Right now an input such as −10,000 results in -10000 B.

Let’s introduce absBytes:

long absBytes = bytes == Long.MIN_VALUE ? Long.MAX_VALUE : Math.abs(bytes);

The complicated expression is due to the fact that -Long.MIN_VALUE == Long.MIN_VALUE. Now we perform all computations related to exp using absBytes instead of bytes.

Final Version

Here’s the final version of the code, golfed and compacted in the spirit of the original version:

// From: https://programming.guide/worlds-most-copied-so-snippet.html
public static strictfp String humanReadableByteCount(long bytes, boolean si) {
    int unit = si ? 1000 : 1024;
    long absBytes = bytes == Long.MIN_VALUE ? Long.MAX_VALUE : Math.abs(bytes);
    if (absBytes < unit) return bytes + " B";
    int exp = (int) (Math.log(absBytes) / Math.log(unit));
    long th = (long) Math.ceil(Math.pow(unit, exp) * (unit - 0.05));
    if (exp < 6 && absBytes >= th - ((th & 0xFFF) == 0xD00 ? 51 : 0)) exp++;
    String pre = (si ? "kMGTPE" : "KMGTPE").charAt(exp - 1) + (si ? "" : "i");
    if (exp > 4) {
        bytes /= unit;
        exp -= 1;
    }
    return String.format("%.1f %sB", bytes / Math.pow(unit, exp), pre);
}

Note that this started out as a challenge to avoid loops and excessive branching. After ironing out all corner cases the code is even less readable than the original version. Personally I would not copy this snippet into production code.

For updated code that is of production quality see separate article: Formatting byte size to human readable format

Key Takeaways

• Stack Overflow snippets can be buggy, even if they have thousands of upvotes.

• Test all edge cases, especially for code copied from Stack Overflow.

• Floating-point arithmetic is hard.

• Do include proper attribution when copying code. Someone might just call you out on it.

Comments (11)

Whoa! What a writeup. Thanks for sharing

by Nick |  Reply

This is a really hard problem.

by Ssuching |  Reply

Brilliant. Attitude too. Thanks a lot.

by syjmick |  Reply

I think key takeaway here is: prefer short and simple loops over math. As you already said, the math is very hard to get exactly right (so, error prone and hard to read). But I believe it is also at least an order of magnitude slower than the loop-based solution.

Did you run any benchmarks?

by Ivan |  Reply

In general I agree with you. In this particular case however, one should note that the rounding error, negative input, and floating-point precision problems would apply also to a simple loop solution.

I have not done any benchmarking. Would be interesting for sure.

by Andreas Lundblad |  Reply

This is fantastically done. Thanks for posting this.

by John Doe |  Reply

This is very interesting article, I worked with floating point but always had difficulty to grasp the special cases of rounding. This article is good academic view of special cases to consider.

Thanks! Five stars for this article. ★★★★★

by Audiory |  Reply

This article was quite a journey! Thanks :)

by swiatek7 |  Reply

Awesome! Thanks for sharing!

by Adam |  Reply

Nice article, thanks for sharing this story! So, how is it done in Unix? Some commands like ls, df have the -h human readable option.

by IvanV |  Reply

The implementation for coreutils is found in human.c

by Andreas Lundblad |  Reply

Add comment