Big O notation explained
Big O notation is a convenient way to describe how fast a function is growing.
When studying the time complexity T(n) of an algorithm it's rarely meaningful, or even possible, to compute an exact result. Typically we are only interested in how fast T(n) is growing as a function of the input size n.
For example, if an algorithm increments each number in a list of length n, we might say: "This algorithm runs in O(n) time and performs O(1) work for each element".
Definition: Let T(n) and f(n) be two positive functions. We write T(n) ∊ O(f(n)), and say that T(n) has order of f(n), if there are positive constants M and n₀ such that T(n) ≤ M·f(n) for all n ≥ n0.
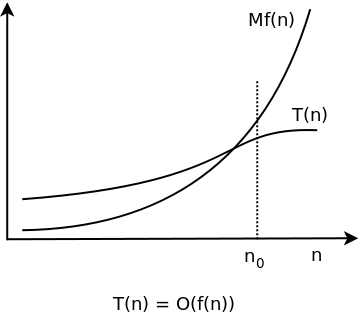
Basically, T(n) ∊ O(f(n)) means that T(n) doesn't grow faster than f(n).
Constant time
Let's start with the simplest possible example: T(n) ∊ O(1).
According to the definition this means that there are constants M and n0 such that T(n) ≤ M when n ≥ n0. In other words, T(n) ∊ O(1) means that T(n) is smaller than some fixed constants, whose value isn't stated, for all large enough values of n.
An algorithm with T(n) ∊ O(1) is said to have constant time complexity.
Linear time
In Time complexity explained we looked at an algorithm max with time complexity T(n) = n -1. Using Big O notation this can be written as T(n) ∊ O(n). (If we choose M = 1 and n₀ = 1, then T(n) = n - 1 ≤ 1·n when n ≥ 1.)
An algorithm with T(n) ∊ O(n) is said to have linear time complexity.
Quadratic time
The algorithm reverse from Time complexity explained had time complexity T(n) = n2/2 - n/2. With Big O notation, this becomes T(n) ∊ O(n2), and we say that the algorithm has quadratic time complexity.
Sloppy notation
The notation T(n) ∊ O(f(n)) can be used even when f(n) grows much faster than T(n). For example, we may write T(n) = n - 1 ∊ O(n2). This is indeed true, but not very useful.
Ω and Θ notation
Big Omega is used to give a lower bound for the growth of a function. It's defined in the same way as Big O, but with the inequality sign turned around:
Definition: Let T(n) and f(n) be two positive functions We write T(n) ∊ Ω(f(n)), and say that T(n) is big omega of f(n), if there are positive constants m and n₀ such that T(n) ≥ m(f(n)) for all n ≥ n₀.
Big Theta is used to indicate that an function is bounded both from above and below:
Definition: T(n): ∊ Θ(f(n)) if T(n) is both O(f(n)) and Ω(f(n)).
Example: T(n) = 3n3 + 2n + 7 ∊ Θ(n3)
- If n ≥ 1, then T(n) = 3n3 + 2n + 7 ≤ 3n3 + 2n3 + 7n3 = 12n3. Hence T(n) ∊ O(n3).
- On the other hand, T(n) = 3n3 + 2n + 7 > n3 for all positive n. Therefore T(n) ∊ Ω(n3).
- And consequently T(n) ∊ Θ(n3).
Key takeaways
When analyzing algorithms you often encounter the following time complexities (in order of growth):
- Θ(1)
- Θ(log n)
- Θ(n)
- Θ(n log n)
- Θ(nk), where k ≥ 2
- Θ(kn), where k ≥ 2
- Θ(n!)
The first four indicate an excellent algorithm:
O(n log n) is really good
An algorithm with worst-case time complexity W(n) ∊ O(n log n) scales very well. The logarithm function grows very slowly:
- log2 1,000 ≈ 10,
- log2 1,000,000 ≈ 20,
- log2 1,000,000,000 ≈ 30.
In fact, O(n log n) time complexity is close to linear: it takes roughly twice the time to solve a problem twice as big.
The last three typically spell trouble:
Ω(n2) is pretty bad
Algorithms with time complexity Ω(n2) are useful only for small input: n shouldn't be more than a few thousand:
- 10,0002 = 100,000,000.
An algorithm with quadratic time complexity scales poorly: if you increase the input size by a factor 10, the time increases by a factor 100.